Last week’s release of the results of the DfE’s new phonics test for six and seven year olds was, when it hit the media, predictably a matter of choosing whether your glass was half full or half empty.

The BBC, perhaps unsurprisingly, fell quickly into line with the right wing press by focussing its headline on the reported failure rate (‘New phonics test failed by four out of 10 pupils’) putting itself in much the same camp as the Daily Mail, which started out by leading on the number of children who failed the test (‘more than 235,000’ – see URL) who, the paper alleged, were struggling to cope with words such as ‘farm’ and ‘goat’ only to switch tack and refocus its headline on the nonsense words included in the test. Elsewhere, the Guardian chose to focus, instead, on talking up the pass rate (‘Three-fifths of six-year-olds reach expected standard in phonics test’), while The Independent was in no doubt whatsoever that any failure attached to these results lies squarely with the tests and not the pupils or teachers (‘The test is at fault, not the kids or the teachers’).

Based on a quick and wholly scientific straw poll of local newspapers, using Google, local papers across England seem to be equally divided on what, if anything, the results of these tests might actually have to tell us about the current state of primary education, all of which tends to suggest that local narratives surrounding schools and school performance have had more to do with the manner in which these results have been reported across the country than any real analysis or understanding of the results themselves.

AS so often seems to be the case, these day, it would appear to have fallen to us humble bloggers to take on the scut work and actually and make sense of the DfE’s results and in that vein I’ve been alerted to what appear to be some fairly obvious anomalies in the overall distribution of test scores, by Dorothy Bishop, anomalies that merit much closer examination.

Like Dorothy, I’ve pulled the DfE’s national test score data into a graph (below – click the graph to embiggen) that shows the distribution of test scores for boys, girls and all pupils and, right from the off, there are a number of curious aspects to this graph which require careful explanation.

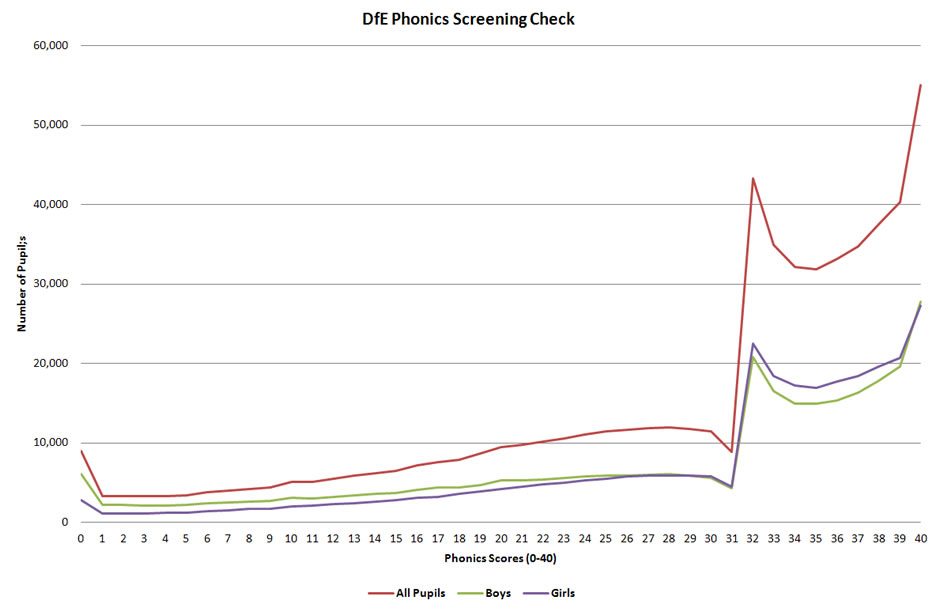
To any kind of stats geek, that distribution looks a little odd. To one with a background in psychology it looks positively bizarre, so much so that it fair screams out that something is very wrong here.

Notwithstanding the fact that reading is a skill that has to be learned, it is still very much a cognitive task and so, if such a task has been subjected to a fair test and the number are large enough (and 580,000 children or so is plenty) then the very first thing you look for in the results is the presence of the normal distribution, the ubiquitous bell curve. Although there are solid mathematical and analytic reasons for the ubiquity of the normal distribution in the social sciences, the main reason that you look for it when you’re looking at data relating to large numbers of humans is simply that the bloody thing turn up just about everywhere, whether you were expecting it to or not. By implication, therefore. when you run across a distribution that so obviously deviates from the normal, as this one does, then there’s clearly some explaining to be done.

As Dorothy correctly points out, for a test of this kind (40 questions marked either right or wrong) what we expect to see when we tabulate the scores from such a large number of tests is a continuous distribution in which the number of pupils obtaining a particular score rises relatively smoothly through a curve to the mode (most common score) before falling away in similarly smooth fashion. Depending on how easy, or difficult, the test is, this distribution may well be skewed towards one side of the graph or the other (left if its difficult, right if its easy) and there is also the possibility of both ceiling and floor effects to take into consideration – and, in fact, the distribution shows both.

We have a small peak at the far left of the distribution where some children scored zero on the test, which is really no more than you’d expect – some kids just can’t read at all for reasons that. most likely, have to do with a cognitive impairment, such as dyslexia, which is still often not diagnosed until children are quite a bit older.

There is also a very obvious ceiling effect here – 9.5% of pupils who took the test (the highest peak on the graph) scored the maximum possible score of 40 on the test, which clearly indicates that pretty sizeable number of kids outperformed the test, in many cases by some considerable distance. This is not quite so problematic as it might at first sound. The phonics test is, after all, intended as a test of basic reading skills, so the fact close to 10% of children got top marks really only tell us that if want a better measure of children’s reading ability at the top end of of the distribution then we need to giving those kids a different, more general, reading test if only to ensure that a command of phonics does genuinely translate into an appropriate level of general reading ability.

Where things get a little strange, however, is when we look at the distribution at or around the ‘pass mark’ for the test, a score of 32 out of 40, a point at which the graph goes completely out of kilter.

Where this leads us, in the first instance, is to an observation about the distribution that’s not, perhaps. immediately obvious from the graph but nevertheless adds some context to the question of the validity of these results, and by extension, the tests themselves and the conclusion that the press have been drawing from them. Put simply, there is the data, a clear suspicion that what we are looking at here are the results of normalised test, i.e. one constructed in such a way that predetermined percentage of children, or at least something close to a predetermined percentage, would be expected to either pass or fail the test.

What creates this suspicion is a rather striking ‘coincidence’. The ‘pass mark’ for the test was a score of 32 correct answers out of 40 and, lo and behold, when we calculate the median score for the distribution we find that that too is 32 out of 40 – the statistical median for the distribution for all children is, in fact, 32.28 with a 0.97 variation in the median score for boys (31.79) and girls (32.76).

Now, on a test administered to a population of just over 580,000 children that is a hell of a coincidence – too much of coincidence, in fact, to be written off as chance, which very strongly suggests that what we are looking at here is test that was designed, in advance, with the clear expectation that somewhere around half the kids taking the test would fail to make the expected grade. In this test, as in most others, you’re not going to be able to normalise the pass mark to get an exact 50-50 pass/fail split because there is insufficient granularity in the test scores to allow for such a close fit – and, in any case, an exact 50-50 split would look just too suspicious to avoid close scrutiny of the results – but it is nevertheless the case that the close correspondence between the median population score and the pass mark for the test that something rather fishy may be going on here.

The suggestion that the test has been normalised to generate a pass/fate rate of somewhere close to 50% fits pretty well with Dorothy’s thoughts on the rather unusual shape of the distribution at and around the pass mark of 32 out of 40:

But there’s also something else. There’s a sudden upswing in the distribution, just at the ‘pass’ mark. Okay, you might think, that’s because the clever people at the DfE have devised the phonics test that way, so that 31 of the items are really easy, and most children can read them, but then they suddenly get much harder. Well, that seems unlikely, and it would be a rather odd way to develop a test, but it’s not impossible. The really unbelievable bit is the distribution of scores just above and below the cutoff. What you can see is that for both boys and girls, fewer children score 31 than 30, in contrast to the general upward trend that was seen for lower scores. Then there’s a sudden leap , so that about five times as many children score 32 than 31. But then there’s another dip: fewer children score 33 than 32. Overall, there’s a kind of ‘scalloped’ pattern to the distribution of scores above 32, which is exactly the kind of distribution you’d expect if a score of 32 was giving a kind of ‘floor effect’. But, of course, 32 is not the test floor.

This is so striking, and so abnormal, that I fear it provides clear-cut evidence that the data have been manipulated, so that children whose scores would put them just one or two points below the magic cutoff of 32 have been given the benefit of the doubt, and had their scores nudged up above cutoff.

Although it does also suggest that she may have been somewhat premature in suggesting that its unlikely that the test has been structured in such a way as to incorporate a precipitous leap in difficult at the test’s pass mark.

If we look at the data for test scores from 4 , where we start to see a rising trend, to 28, where the distribution peaks naturally before the pass mark, the average increase in the number of children attaining a particular score is around 360 per mark. Although this trend does fall away between 29 and 31, the fall off is relatively small from 28 to 30 (around 550) and drops sharply (by 2,600) only at a score of 31, one mark below the pass mark. Taking into account the rising trend between 4 and 28, the discrepancy in the result just before the pass mark is around 4,500 to 5,000 – that’s the number of kids who we’d expect to have been marked more leniently by their teachers on a couple of words in order to bump them up to the pass mark.

Against this, the actual increase in the distribution from 31 to 32 is almost 34,500 and even if we adjust from the projected trend from 28 to 31, nullifying the effect of teachers gaming the test, we’d still be looking at a rise of around 26,000 and a little over three times as many children achieving the pass mark as achieved one mark below the pass mark. Even for a skewed distribution, that’s still quite a leap over the space of single mark on a right/wrong answer, which rather tends to suggest that the test may well have been designed to include a substantial leap in difficulty somewhere close to median ability.

Is it feasible for the DfE to have ‘cooked’ the test in advance to produce something close to a predetermined outcome?

Yes.

First and foremost, the background resources provided by the DfE include this technical description of the structure of the test and the criteria for the expected minimum standard that children should reach in order to pass the test:

In particular this means that in the screening check, a pupil working at the minimum expected standard should be able to decode:

– all items with simple structures containing single letters and consonant digraphs

– most items containing frequent and consistent vowel digraphs

– frequent means that the vowel digraph appears often in words read by pupils in year 1

– consistent means the digraph has a single or predominant phoneme correspondence

– all items containing a single 2-consonant string with other single letters (i.e., CCVC or CVCC)

– most items containing two 2-consonant strings and a vowel (i.e., CCVCC)

– some items containing less frequent and less consistent vowel digraphs, including split digraphs

– some items containing a single 3-consonant string

– some items containing 2 syllables

It should be noted that items containing a number of the different features listed above will become more difficult. It will become less likely that a pupil working at the minimum expected standard will be able to decode such items appropriately. For example, a pupil will be less likely to decode an item containing both a consonant string and a less frequent vowel digraph, than an item with a consonant string but a frequent, consistent vowel digraph.

That last paragraph is particularly important as it clear indicates how it is possible to substantially ratchet up the difficulty of the test at a particular point by including words that combine several features from the core list into a single word.

Moreover, in terms of pinpointing exactly where in the test one should start to ratchet up the difficulty in order to generate a particular outcome, the DfE had the data from a pilot study to pilot study to work with in which 360 test words were put to around 1,000 pupils at 30 schools, which is a large enough sample to generate sufficient data to normalise the final test with a good degree of accuracy. Noticeably, although the DfE has published an evaluation of the pilot, this was only a process evaluation and does not include any of the data from the actual testing, so we’ve no way of knowing exactly how the children in the pilot performed or, for the time being, of analysing the results generated by the pilot in terms of children’s performance on particular types and combinations of phonemes and phonetic structure and relating these to the structure and results of the actual tests used in schools.

Given the unusual and rather questionable nature of the distribution of results generate by the new test when it was applied to the general school population and the apparent normalisation of the test to the median – and notwithstanding any of the concerns that have been raised about the questionable validity of the government’s decision to implement a phonics first and fast approach to early years reading – the results of this years test would appear to require much closer scrutiny, particularly of the underlying structure of the test and how this relates to the detailed data from the pilot.

Until we get such an in-depth analysis, which will require both the involvement of a linguistics specialist and, no doubt, a number of searching FOI requests to unshackle the relevant data, the validity of the new phonics testing system must remain in serious doubt, so much so that nothing of any consequence can reasonably be read into this year’s results, not least as it appears that both the DfE and teachers may have been involved in gaming the results.